| (解答) |
| |
| (1)と(2)はよく似た問題ですが、たさなければならない数の傾向が異なるため、計算の工夫も異なります。 |
| |
| (1) |
(16+82+67+48+91+33+29+75+54)÷9 |
| |
1の位と10の位、それぞれたして10になる組み合わせを見つけます。 |
| |
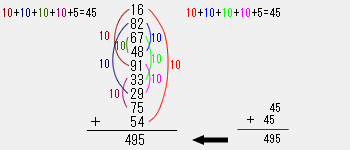 |
| |
(16+82+67+48+91+33+29+75+54)÷9 |
| = |
495÷9 |
| = |
55 |
| (2) |
(55+49+59+54+60+52+58+57+51)÷9 |
| = |
50+(5-1+9+4+10+2+8+7+1)÷9 |
| = |
50+45÷9 |
| = |
55 |
| |
|
| (解説) |
| |
| (1),(2)ともに平均を求めるときに出てくる計算式です。 |
| 結果は同じ答えになりますが、 |
| (1)は、基準となる数を設定するのが難しいため、各々の数をそのままたしてから割らざるをえません。 |
| (2)は、いずれも50前後の数であるため、50を基準にして、50との差をプラスマイナスして、その平均を求めれば、簡単に求めることができます。 |
| |
| 平均の問題で、似たような数の平均を求める場合は、(2)の方法を使ってください。 |
| |
| ← 問題に戻る 次の問題 → |
| |